- Thu 06 April 2017
- brightway2

Faster sparse linear algebra
Adrian Haas, a PhD student at ETH Zürich, has written a Python wrapper to the Pardiso multicore sparse solver, which conveniently is include in the Intel math kernel library which comes in Conda. He has also packaged his wrapper on Anaconda, and it is now used by default when you install Brightway via conda.
There is an additional benefit to Adrian's work, aside from the raw speed increase - his wrapper always keeps the LU factorization of the matrix, so you don't have to think about whether or not to pass factorize=True.
Faster row and column indexing
The processed arrays that are used to build matrices don't have row and column values filled in already. Instead, these values must be calculated dynamically based on the databases used. After Adrian implemented pypardiso, this indexing step - going from internal dataset ids to row and column values - was taking around two thirds of the time to do an LCA calculation. I had implemented the bw2speedups library, which uses Cython to speed up some Numpy operations. However, the algorithm in bw2speedups still did a dictionary lookup for each element in the processed array. Thanks to some smart people on the internet, we can use the fact that we have Numpy arrays to make things go much quicker.
Indexing when we don't already have row or column dictionaries
When we first get started, we don't have dictionaries that link internal dataset ids (say, 42) to row or column indices (say, 0). We can then use the index_with_searchsorted function, which looks like this:
unique = np.unique(array_from)
idx = np.searchsorted(unique, array_from)
array_to[:] = idx
return dict(zip(
(int(x) for x in unique),
itertools.count()
))
This looks like some deep magic, so let's go through it line by line. We start with an array of essentially random numbers, array_from:
import numpy as np
array_from = np.random.randint(10, 20, size=20)
=> array([19, 10, 13, 18, 13, 19, 12, 16, 12, 19, 17, 10, 16, 15, 13, 10, 19,
13, 10, 13])
We first create unique, which is a sorted array of unique values from array_from. The result in this trivial case is not so surprising:
unique = np.unique(array_from)
=> array([10, 12, 13, 15, 16, 17, 18, 19])
Now we use searchsorted. To be honest, I didn't even know such a function existed, and I certainly would not have thought of applying it in this case. It still somehow seems like a bit of magic to me.
idx = np.searchsorted(unique, array_from)
=> array([7, 0, 2, 6, 2, 7, 1, 4, 1, 7, 5, 0, 4, 3, 2, 0, 7, 2, 0, 2])
The docstring for searchsorted is rather mysterious: "Find indices where elements should be inserted to maintain order." After some contemplation, and maybe some meditation on the nature of numerical algorithms and the universe, it begins to make more sense. We want to take each element from array_from, and figure out the index (i.e. index 0 would be the first element in the array) where we could insert this element, so that unique would stay in the same order. We benefit from the fact that the insertion indices will start at zero and go up, and this is exactly how our row and column indices behave as well. So we can use these insertion indices as our row and column values without doing anyting extra!
The next line, array_to[:] = idx, just inserts our new indices into our target array, and we return a dictionary that maps values in array_from to our row or column indices:
{10: 0, 12: 1, 13: 2, 15: 3, 16: 4, 17: 5, 18: 6, 19: 7}
This all seems a bit complicated. Why would it be faster than dictionary lookups, which we know are really fast™? The answer is that operations on Numpy arrays aren't interpreted in Python, but happen in C code, making them almost the same speed for an array of one million numbers as for an array of one number. Contrast this with the previous approach; while dictionary lookups are fast, we would still need to do one lookup for each element in the array, of which there are many.
Indexing when we do already have row or column dictionaries
It gets a little harder when we already have a row or column dictionary. Let's continue out example and see how the function index_with_arrays would work with a different input array:
keys = np.array(list(mapping.keys()))
values = np.array(list(mapping.values()))
if keys.min() < 0:
raise ValueError("Keys must be positive integers")
index_array = np.zeros(keys.max() + 1) - 1
index_array[keys] = values
mask = array_from <= keys.max()
array_to[:] = -1
array_to[mask] = index_array[array_from[mask]]
array_to[array_to == -1] = MAX_INT_32
In this case, we are given a mapping of dataset ids to row or column indices: {10: 0, 12: 1, 13: 2, 15: 3, 16: 4, 17: 5, 18: 6, 19: 7}. We also have an input array:
array_from = np.array([1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21])
We need to create a general purpose algorithm, so we can't make any assumptions about the input values. They can (and in real life will) be outside the range of our mapping dictionary.
We start by turning mapping into two arrays:
keys = np.array(list(mapping.keys()))
values = np.array(list(mapping.values()))
=> (array([16, 17, 18, 19, 10, 12, 13, 15]), array([4, 5, 6, 7, 0, 1, 2, 3]))
Dictionaries are unordered, but we know that iterating over keys() and values() will proceed in the same order. After a validity check, we create the index_array - a temporary array we will insert values into. We also set everything in this array to -1, which will be our dummy value to indicate that this element is missing (we can't use 0 as a dummy value, as this is a real row or column index).
index_array = np.zeros(keys.max() + 1) - 1
=> array([-1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1., -1.,
-1., -1., -1., -1., -1., -1., -1.])
Next, we do a step that exposes the power of Numpy arrays, but can be a bit tricky to parse at first. We know that our dataset ids are integers, and while they don't have any real meaning, we can conceptualize them not as random values, but as indices into an array. So, instead of dataset id 42 being a row number in a SQLite database, we will treat it as an index into an array, and it will be used to return index_array[42].
You might think that this is inefficient - we might have to create an array of thousands of elements to store only a few. We know, however, that dataset ids are relatively small, probably much less than 100.000 in any given project. So we can create a temporary array index_array with 100.000 elements, use it, and then throw it away almost instantaneously.
But we still need to make index_array useful. To do that, we populate it with the row and column indices:
index_array[keys] = values
=> array([-1., -1., -1., -1., -1., -1., -1., -1., -1., -1., 0., -1., 1.,
2., -1., 3., 4., 5., 6., 7.])
This is the same as looking up each value in mapping, as in the following loop, but it is much more efficient due to working with arrays:
for key, value in mapping.items():
index_array[key] = value
The key (sorry, bad pun) is remember that we are treating the dataset id values as indices into index_array.
We can then create a boolean mask of where our input data is in the valid mapping range (we only need to check the top end - we assume that values in array_from are always >= zero).
mask = array_from <= keys.max()
=> array([ True, True, True, True, True, True, True, True, True,
True, False], dtype=bool)
We also reset our target array to be -1:
array_to[:] = -1
And we are ready for the magic of index_array. We treat our input array array_from not as data but as integers into index_array`, and then assign the resulting row or column indices to the correct positions in array_to:
array_to[mask] = index_array[array_from[mask]]
=> array([-1., -1., -1., -1., -1., -1., 2., 3., 5., 7., -1.])
Finally, we set all values in the target array which were -1 to a dummy value that indicates that the input values were not present in the mapping dictionary:
array_to[array_to == -1] = MAX_INT_32
These elements won't be used in any built matrices.
Will it blend?
How much faster will these two changes make normal LCA calculations? We already knew that the default solver in Scipy, SuperLU, is slower than UMFPACK; that is why the installation of scikit-umfpack was already recommended. UMFPACK also has cool new features for using GPUs and multithreading (SuperLU also has a branch for multithreading), but these new developments have not made it into the Python wrappers. So, in total, we have four alternatives to compare: SuperLU, UMFPACK, Pardiso, and Pardiso with indexing improvements. I calculated the time to solve the inventories for 250 activities chosen at random from ecoinvent 3.3 cutoff, and while the time to solve each functional unit varied, the pattern is quite clear:
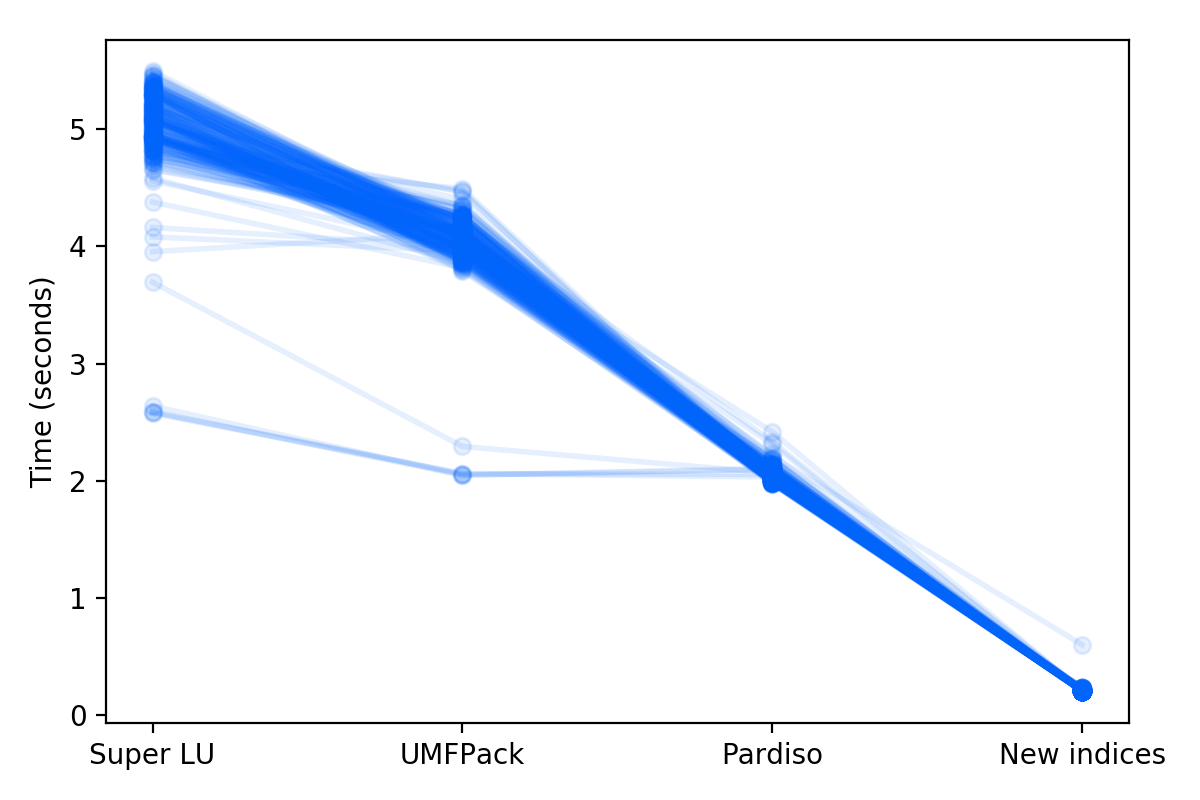
There is a limitation here - the indexing improvements only apply when the matrices are first created, so there is no speed gain for repeated calculations using different functional units or during Monte Carlo calculations.